I. Einführung
Im ersten Teil unseres Forschungsabenteuers haben wir die Grundlagen der Information-Bottleneck (IB) Theory behandelt. Wir haben gesehen, wie die Theorie zu einem besseren Verständnis von Deep Learning (DL) beiträgt, indem sie zwei Variablen nutzt – nämlich jene für die beiden Achsen der sogenannten Informationsebene. So wird das Bild eines künstlichen neuronalen Netzwerks (KNN) vermittelt, ohne dass dafür auch die unzähligen Verbindungsparameter eines solchen Netzwerks dargestellt werden. Schlussendlich haben wir die bemerkenswerte Ähnlichkeit zwischen den Achsen der Informationsebene und den makroskopischen Variablen in der statistischen Thermodynamik gesehen.
In diesem zweiten Teil steigen wir nun noch tiefer in die IB-Theorie ein. Dieser Blogpost ist dabei die kürzere, nicht-mathematische Version eines sehr ausführlichen Beitrags, den ich vor einigen Wochen – auf Englisch – geschrieben habe. Zunächst werde ich untersuchen, welche Rolle die Menge an verwendeten Trainingsdaten beim Deep Learning spielt. Wir werden dann sehen, dass die zwei Phasen bei einem stochastischen Gradientenabstieg den Drift- und Diffuisons-Phasen der sogenannten Fokker-Planck-Gleichung ähnlich sind. Dies ist eine weitere Übereinstimmung mit der statistischen Mechanik.
II. Die Rolle der Trainingsdaten – wie viel ist genug
Zu den wichtigsten Ergebnissen aus der IB-Theorie zählt, dass das Deep Learning aus zwei Phasen besteht – der Anpassungs- und der Kompressionsphase. Wir konnten im letzten Teil dabei beobachten, dass verschiedene randomisierte Netzwerke denselben Kurvenverlauf auf der Informationsebene in denselben Phasen beschreiben. Indem ein Durchschnittswert für diese Kurven verschiedener Netzwerke gebildet wird, ergibt sich eine Darstellung wie jene in Abbildung 1.

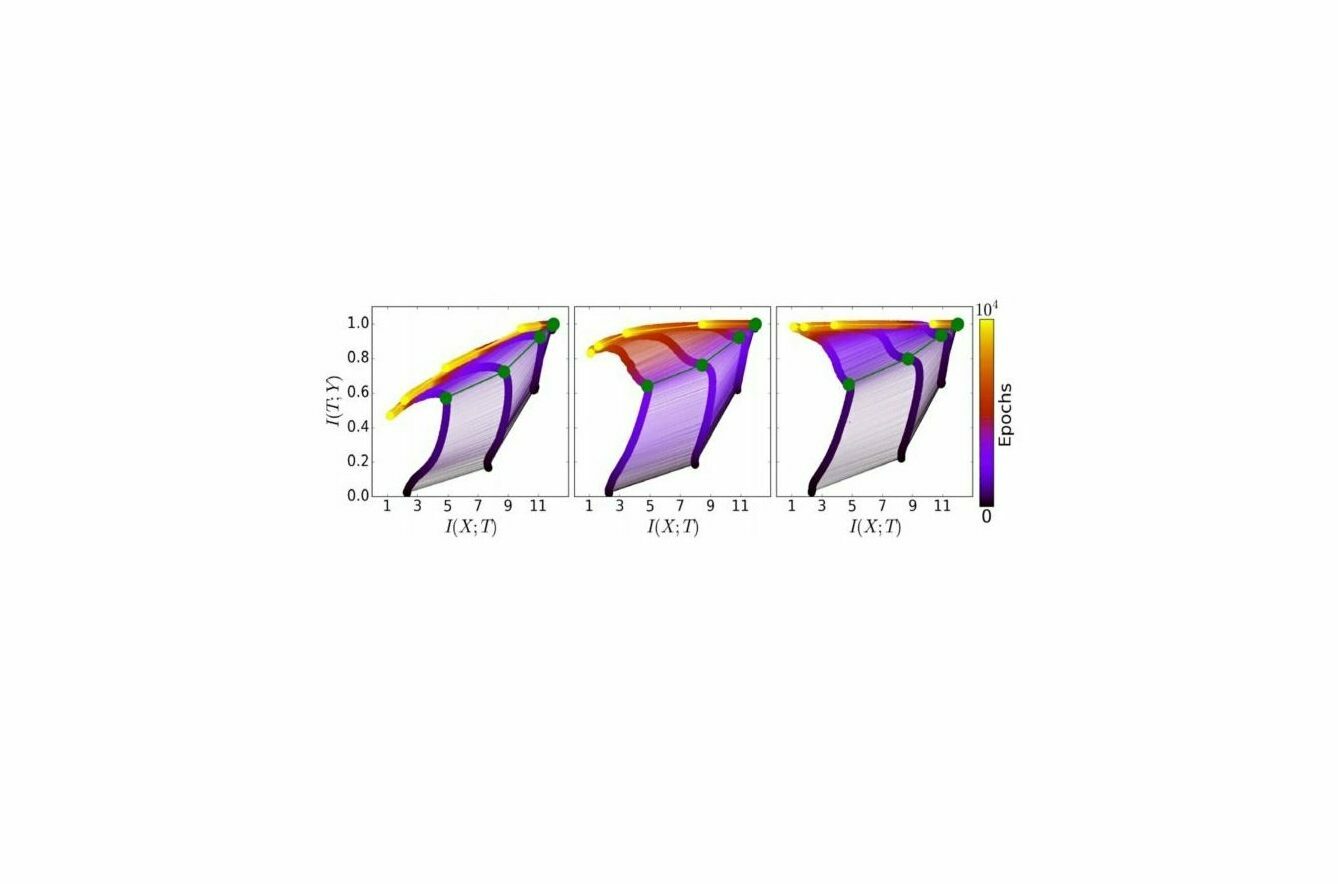
Abbildung 1: Die Entwicklung der Schichten während des Trainingsprozesses in der Informationsebene – jeweils für verschiedene Trainingsmuster. Links: 5 Prozent der Daten; Mitte: 45 Prozent der Daten; rechts: 85 Prozent der Daten. Die Farben geben die Anzahl der Trainingsdurchläufe über den jeweiligen Trainigs-Datensatz mit stochastischem Gradientenabstieg von 0 bis 10 000 an. Die grünen Pfade entsprechen dem SGD-Drift-Diffusions-Phasenübergang. Abbildung und Bildunterschrift von R. Schwarz-Ziv et al., 2017. Hier werden auch weitere Details über die verwendete Netzwerkarchitektur und der eigentlichen Natur der Trainingsdaten besprochen.
Die Abbildung zeigt die Trainingsdynamik für randomisierte KNNs für fünf Prozent (links), 45 Prozent (Mitte) sowie 85 Prozent (rechts) der Trainingsdaten. Die Anpassungsphase ist in allen drei Fällen gleich, wie Sie auf der x-Achse sehen können. Wenn wir jedoch mehr Daten in das Training einbeziehen – wie das Beispiel mit den 85 Prozent (rechts) zeigt – verändert sich die Kompressionsphase, die auf der y-Achse dargestellt wird.
Kleine Sätze von Trainingsdaten – wie zum Beispiel mit den 5 Prozent (links) – führen zu einer größeren Kompression. Das ist ein Zeichen für Über-Anpassung. Daher hilft die Kompression zwar, die schichtweise Repräsentation innerhalb der KNN zu vereinfachen – sie kann aber auch zu einer zu starken Vereinfachung führen. Die richtige Balance zwischen der Vereinfachung und dem Verlust von zu viel relevanten Informationen zu finden, bleibt daher noch Gegenstand weiterer Untersuchungen von Tishby und anderen Forschern.
III. Ein Gedankenexperiment – Exkursion in die statistische Mechanik
Lassen Sie uns einen Schritt zurücktreten und über etwas anderes sprechen. Wobei: Vielleicht ist es gar nicht so anders? Lassen Sie uns ein Gedankenexperiment machen.
III.1. Drift und Diffusion – Oder: die Farbe im Wasserglas
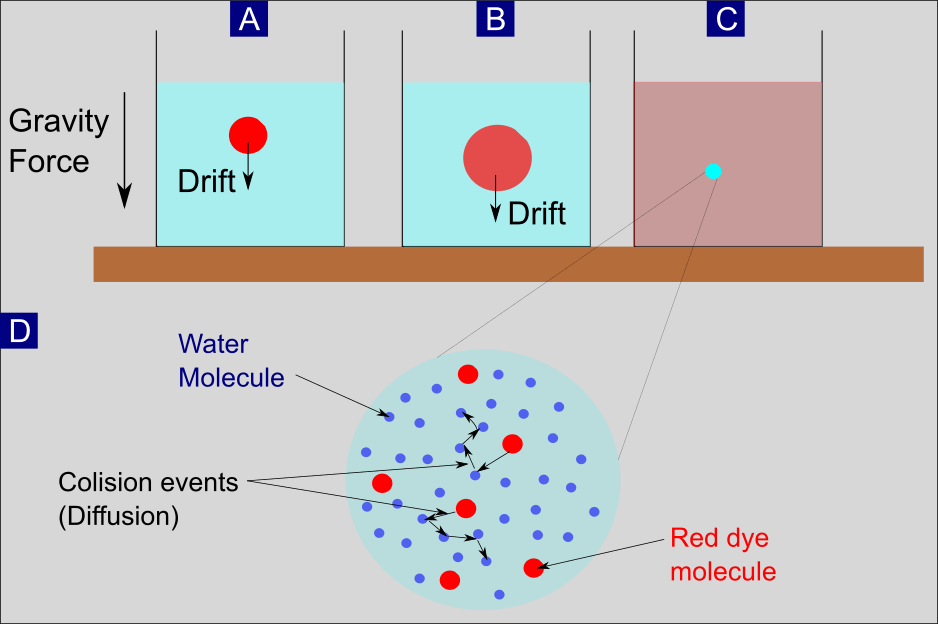
Abbildung 2: Schema des Drift- und Diffusionsprozesses. (A) Roter Farbstoff, der in einem Wasserglas gelöst ist und (im Mittel ) als Ganzes aufgrund der Schwerkraft nach unten driftet. (B) Farbstoffmoleküle, die in das umgebende Wasser auseinander laufen. Sie besetzen ein immer größeres Volumen aufgrund eines Prozesses, der Diffusion genannt wird. (C) Diffusion und Drift führten zu einer homogenen Verteilung des roten Farbstoffs im Wasser. (D) Vergrößerung von einem kleinen Bereich im Wasserglas, nachdem der homogene Zustand erreicht ist. Zu sehen ist der Prozess der Diffusion, dargestellt durch zufällige Kollisionsereignisse einzelner Farbstoffmoleküle mit umgebenden Wassermolekülen.
Stellen Sie sich vor: Wir nehmen ein Glas und befüllen es mit Wasser. Anschließend lösen wir einen Tropfen roten Farbstoffs im oberen Bereich des Wassers auf (Abbildung 2A). Aufgrund der Gravitationskraft driftet der Farbtropfen mit der Zeit mehrheitlich in Richtung Grund. Durch einen Prozess, der Diffusion genannt wird, nimmt das Volumen der Farbmoleküle zugleich zu (Abbildung 2B). Letztlich sorgen der Drift und die Diffusion dafür, dass sich die Farbmoleküle gleichmäßig im Wasser verteilen. Angemerkt werden muss dabei: Es ist bereits ein Drift ohne irgendein äußeres Kraft-Potential wie die Gravitation vorhanden – allein aufgrund der Reibungskraft (Details dazu in der Langfassung). Die Erwähnung der Schwerkraft als externer Kraft dient in diesem Zusammenhang nur dazu, den Sachverhalt zu veranschaulichen.
III.2. Einzelne Partikel kontra ein Zusammenspiel von Partikeln – die zwei Seiten derselben Medaille
Wie sollen wir diese beiden Prozesse nun verstehen? Wo fangen wir an? Sollten wir versuchen zu verstehen, wie sich die einzelnen Farbmoleküle verhalten? Oder sollten wir vielmehr fragen, wie sich die Summe – also der Farbtropfen insgesamt – verhält? Solche Fragen stehen im Mittelpunkt der statistischen Mechanik. Bei ihr betrachten wir die Dynamik von Systemen, die sich aus einer riesigen Menge von einzelnen Partikeln zusammensetzen. Die Anwendung statistischer Mechanik auf diese Systeme zeigt im Wesentlichen, dass die mikro- und makroskopische Beschreibung einander entsprechen.
Schon in der Römerzeit beschäftigten sich die Denker mit der Wechselwirkung von Individuen und Gruppen. In seinem naturwissenschaftlichen Gedicht De rerum natura aus dem ersten Jahrhundert v. Chr. beschreibt der römische Dichter und Philosoph Lucrectius ein Phänomen, das heute als Brownsche Bewegung bekannt ist. Lucrectius führte die scheinbar zufälligen Bewegungen einzelner Staubteilchen auf die Kollision mit Luftmolekülen zurück, die sie umgeben. Für Lucrectius war dies der Beweis, dass Atome existieren. Um genau zu sein: Seine Darstellung umfasste nicht nur den zufälligen Teil der Bewegung, sondern auch den deterministischen Teil der Dynamik. Dieser wird durch Luftströme verursacht und ist vergleichbar mit der Drift-Dynamik aus unserem Gedankenexperiment. Der zufällige Teil der Bewegung wiederum wird zu Ehren des schottischen Botanikers Robert Brown als Brownsche Bewegung bezeichnet. Eine Simulation der Brownschen Bewegung ist in Abbildung 3 zu sehen.

Abbildung 3: Simulation der Brownschen Bewegung von fünf Partikeln (gelb), die mit einer großen Ansammlung von 800 Partikeln kollidieren. Die gelben Partikel hinterlassen fünf blaue Spuren beliebiger Bewegungen. Eine davon hat einen roten Geschwindigkeitsvektor. (Quelle: Wikipedia)
III.3. Die Einzelteilchen-Perspektive – Stochastische Differentialgleichungen
Die Dynamik einzelner Partikel wird bei der Brownschen Bewegung mathematisch durch eine stochastische Differentialgleichung (SDG) beschrieben. Vereinfacht gesagt ist das eine Differentialgleichung, bei der mindestens ein Term in der Gleichung ein stochastischer Prozess ist. Durch ein System von SDGs können wir Tausende oder auch Millionen von Molekülen simulieren, die sich in einem Glas mit einer weiteren Million bis Milliarde kleinerer Wassermoleküle bewegen. Am Anfang könnten die größeren Partikel in einem kleinen Bereich des Wassers konzentriert sein (wie in Abbildung 1). Im weiteren Verlauf bestimmt dann aber eine jeweils individuelle SDG die zeitliche Dynamik für jedes Partikel. So ein Geschehen abzubilden, wird über die Monte-Carlo-Methode möglich – einen wichtigen Berechnungsalgorithmus in der statistischen Mechanik.
III.4. Eine zusammenfassende Beschreibung – die Fokker-Planck-Gleichung
Aber was passiert, wenn wir herauszoomen aus der mikroskopischen Ansicht? Aus dieser höheren Perspektive betrachtet verwischen die Millionen von Partikel und wir erhalten ein gröberes Bild des Ganzen. Die mathematische Beschreibung ändert sich auch: Statt eines Systems von Millionen von SDGs erhalten wir eine einzige deterministische partielle Differentialgleichung. Sie beschreibt die makroskopische Verteilung aller Partikel in Raum und Zeit. Diese makroskopische Entwicklungsgleichung ist auch bekannt als Fokker-Planck-Gleichung. Obwohl die zeitliche Entwicklung für jedes einzelne Teilchen zufällig ist, entwickelt sich die Menge der Teilchen dennoch deterministisch. Das ist der entscheidende Punkt an dieser Stelle.
Die Fokker-Planck-Gleichung wurde erstmals von dem niederländischen Physiker und Musiker Adriaan Fokker und dem berühmten deutschen Physiker Max Planck aufgestellt, um die Brownsche Bewegung aus einer zusammenfassenden Perspektive zu beschreiben. Sie ist aber auch als Kolmogorov-Gleichung bekannt und geht auf den russischen Mathematiker Andrey Kolmogorov zurück. Er entwickelte die Gleichung 1931 unabhängig von Fokker und Planck.
III.5. Die Fokker-Planck-Gleichung als Kontinuitätsgleichung
Es gibt eine optisch ansprechende Darstellung der Fokker-Planck-Gleichung in der Form einer Kontinuitätsgleichung. Ohne sie hier groß im Detail auszuführen, können wir die Kontinuitätsgleichung leicht durch ein schematisches Bild wie in Abbildung 4 veranschaulichen. Wir sehen die zuvor schon in Abbildung 2d gezeigte Prozess der Diffusion. Zur reinen Illustration wird hier ein innerer Kreis durch eine gestrichelte schwarze Linie von einem äußeren Kreis getrennt. Beschreiben wir die Dichte der roten Farbteilchen im inneren Kreis als p(x,t), dann verändert sich diese Dichte über die Zeit hinweg durch einen Fluss von Teilchen j(x,t), die die gestrichelte Grenze passieren. Eine prosaischere Aussage der Kontinuitätsgleichung kann daher sein: Was hereinkommt, fließt von außen nach innen und analog umgekehrt.
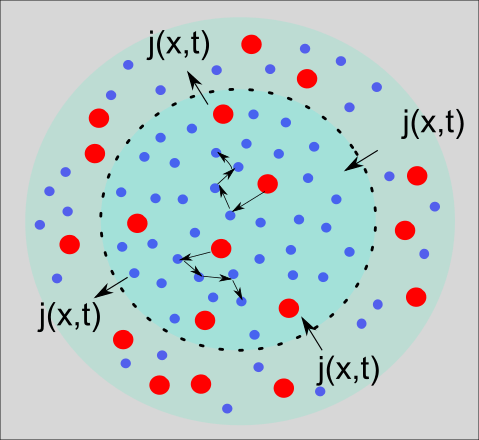
Abbildung 4: Schematische Darstellung der Kontinuitätsgleichung.
IV. Zurück zu IB Theorie – Konstruktion der Analogie
Nach dieser Tour de Force durch die statistische Mechanik von Drift- und Diffusionsprozessen stellt sich natürlich die Frage, wie uns das alles hilft, Deep Learning besser zu verstehen.
Das Training von neuronalen Netzen wird oft nacheinander auf Untermengen des ganzen Trainingsdatensatzes durchgeführt und über den stochastischen Gradientenabfall (SGA) optimiert. Tishby und seine Kollegen haben in ihrer Arbeit 2017 ein schönes Bild präsentiert, dass die Drift- und Diffusionsphasen während der SGA-Optimierung zeigt. Dazu berechneten sie für jede Schicht des KNN den Mittelwert und die Standardabweichungen der gewichteten stochastischen Gradienten und zeichneten diese anschließend als Funktionen der Trainingsdurchläufe auf (Abbildung 5).
Insbesondere ist hier der Übergang von der Anpassungsphase zur Kompressionsphase sichtbar (die vertikale gestrichelte Linie in Abbildung 5). Zu Beginn der ersten Phase (bis zu 100 Trainingsdurchläufe) liegen die Mittelwerte der Gradienten etwa zwei Messeinheiten über den Standardabweichungen. Zwischen dem 100. und dem 350. Trainingsdurchlauf jedoch nimmt die Fluktuationen kontinuierlich zu, bis sie am Übergang schließlich den Mittelwerten entsprechen.
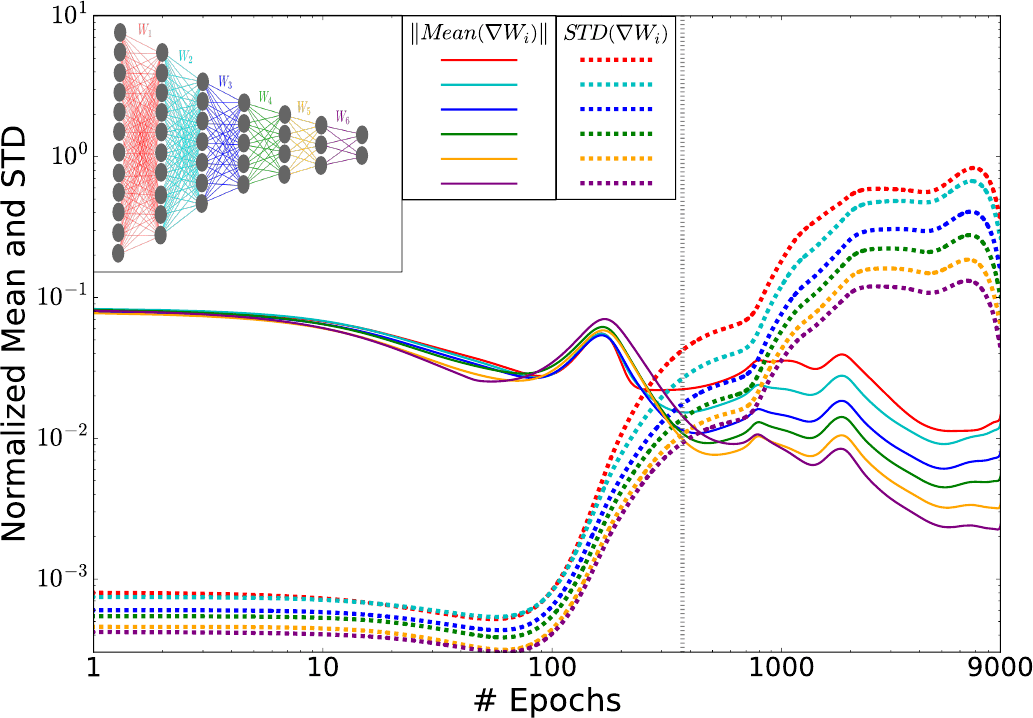
Abbildung 5: Stochastische Gradientenverteilungen der verschiedenen Schichten während des Optimierungsprozesses. Die Norm der Mittelwerte und Standardabweichungen der Gewichtsgradienten für jede Schicht, als Funktion der Anzahl der Trainingsdurchläufe (in log-log-Skala). Die Werte werden durch die L2-Normen der Gewichte für jede Schicht normalisiert, die während der Optimierung signifikant ansteigen. Die graue Linie (∼350 Durchläufe) markiert den Übergang zwischen der ersten Phase mit großen Gradientenmittelwerten und kleiner Varianz (Drift, hoher Gradient SNR: Signal-to-Noise-Ratio) und der zweiten Phase mit großen Fluktuationen und kleinen Mittelwerten (Diffusion, niedriger SNR). Beachten Sie, dass der Gradientenlog (SNR) (die logarithmischen Differenzen zwischen dem Mittelwert und den STD-Linien) sich einer Konstante für alle Schichten nähert, was die Konvergenz des Netzwerks zu einer Konfiguration mit konstantem Fluss relevanter Informationen durch die Schichten widerspiegelt. Abbildung und Bildunterschrift aus R. Schwarz-Ziv et al., 2017.
In der langen Fassung dieses Blog-Beitrags habe ich ein Ableitungsschema einer N-Schichten-Fokker-Planck-Gleichung für die Gewichtung der Schichten skizziert und gezeigt, dass sich die beiden Phasen beim Deep Learning mit den Drift- und Diffusionstermen aus der Fokker-Planck-Gleichung beschreiben lassen. Während der Drift-Term dann von den Gradientenmittelwerten abhängt, wird der Diffusionsterm von den Standardabweichungen der Gewichtsgradienten beeinflusst, genau wie es nach Abbildung 5 zu erwarten war.
V. Zusammenfassung und Ausblick
V.1. Die Rolle des Umfangs der Trainingsdaten
Mit diesem zweiten Teil zur IB-Theorie haben wir zunächst die Frage diskutiert, welche Rolle der Gesamtumfang der Trainingsdaten für das endgültige Trainingsergebnis spielt. Nach der IB-Theorie haben wir gelernt, dass die Anpassungsphase immer gleich ist – unabhängig davon, wie viele Daten wir im Training berücksichtigen. Im Gegensatz dazu spielt der Umfang der Trainingsdaten sehr wohl eine Schlüsselrolle für den Erfolg der Kompressionsphase. Im Wesentlichen führt eine sehr geringe Menge an Trainingsdaten (z.B. nur 5 Prozent) zu einer Überkomprimierung der Informationen.
V.2. Analogie zur Fokker-Planck-Gleichung
Anschließend arbeiteten wir die Übereinstimmung zwischen den beiden Phasen beim Deep Learning und den Drift- und Diffusionstermini der Fokker-Planck-Gleichung (FP) heraus. Die FP-Gleichung ist in der statistischen Mechanik weit verbreitet. Dies wurde insbesondere im Zusammenhang mit der Brownschen Bewegung größerer Teilchen in einer Flüssigkeit veranschaulicht. Eine Detaillierte Erörterung, in welchem Sinne die Gewichtsgradienten für die einzelnen Schichten des neuronalen Netzwerks in eine N-Schichten-FP-Gleichung einfließen, können in der Langfassung dieses Artikels eingesehen werden.
V.3. Was erwartet uns noch?
Als nächstes werden wir uns in einem dritten Teil über die Rolle der verborgenen Schichten unterhalten. Es ist schon seit längerer Zeit bekannt, dass eine einzige verborgene Schicht ausreicht, um eine Funktion von beliebiger Komplexität auf zugrundeliegende Trainingsdaten abzubilden. Eine wichtige Frage in diesem Zusammenhang ist daher: Warum werden immer mehr verborgene Schichten in Betracht gezogen? Wir werden sehen, dass nach der IB-Theorie der Hauptvorteil der zusätzlichen verborgenen Schichten lediglich rechnerischer Natur ist. Das bedeutet, dass sie nur dazu dienen, die Rechenzeit während des Trainings zu verringern. Zusätzlich werden wir im nächsten Teil einige Unzulänglichkeiten der IB-Theorie untersuchen und einem neuen Ansatz nachgehen, der Antworten auf einige dieser Unzulänglichkeiten bietet. Dieser Ansatz wird Variational IB-Theory genannt.